小九的酒窝

之前写了并查集的按秩优化，也就是按照size或者按照rank优化。
我们看下find函数，每次都要一步一步向上查找，直到根节点，如果find函数使用次数非常多的时候，每次都要查找好多次，时间复杂度为O(logn)，但是如果我们直接把所有子结点全部指向根节点的话，也就是说这个时候，树已经变成了两层，查询起来，只需要查询一次就能查找到根节点。就向下图中的那样


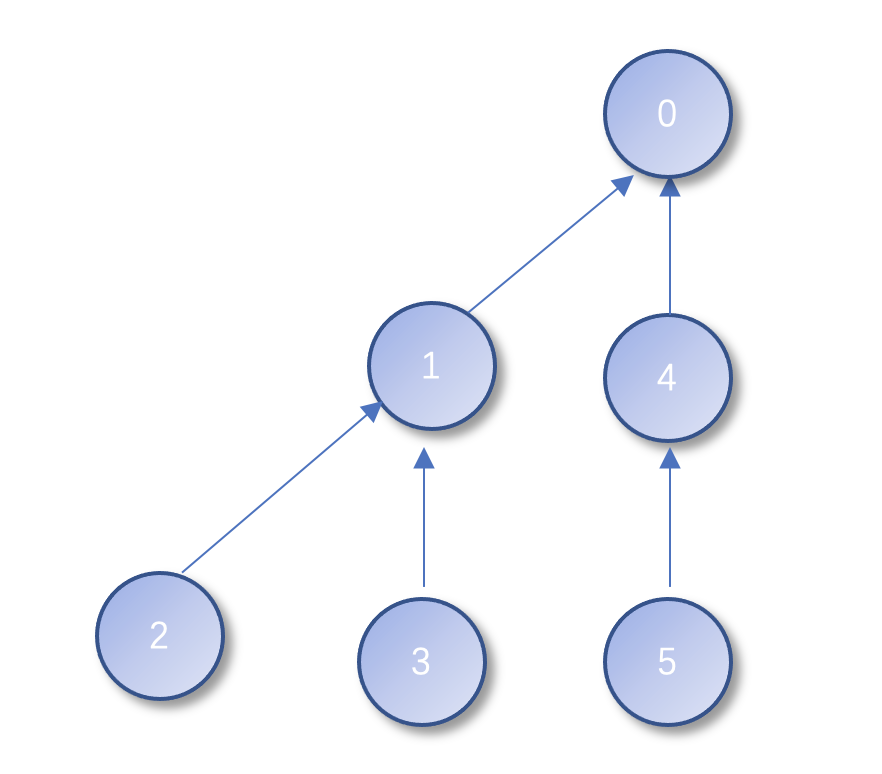
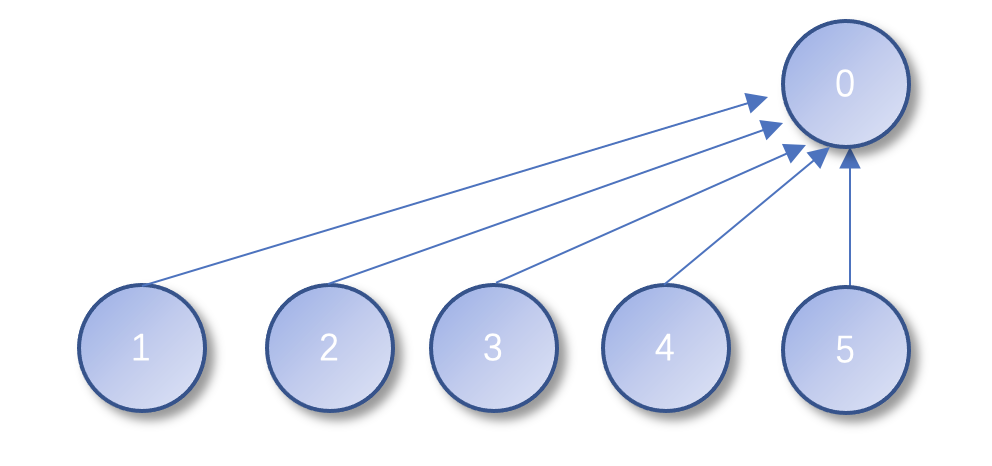
减少树的层数，这个过程就叫做路径压缩。

这里我们可以使用递归来执行，终止条件是查询到根节点，非终止条件的传递操作就是将parents里该节点的设定成父节点的父节点。
路径压缩在我们处理加权并查集的时候会使用到，这里我们再使用按秩优化，顺便加上权，代码如下：
基础数据

• // 树
• int[] parents;
• // 权
• double[] weights;
• // 秩
• int[] size;

初始化方法

        public UnionFind(int n) {
            this.parents = new int[n];
            this.weights = new double[n];
            this.size = new int[];
            for (int i = 0; i < n; i++) {
                parents[i] = i;
                weights[i] = 1.0d;
                size[i] = 1;
            }
        }

find函数

     public int find(int x) {
            assert (x<0 || x >= parents.length);
            if (x != parents[x]) {
                int origin = parents[x];
                parents[x] = find(parents[x]);
                weights[x] *= weights[origin];
            }
            return parents[x];
        }

union函数

        public void union(int x, int y, double value) {
            int xRoot = findRoot(x);
            int yRoot = findRoot(y);
            if (xRoot != yRoot) {
                if (size[xRoot] > size[yRoot]) {
                    parents[yRoot] = xRoot;
                    size[xRoot] += size[yRoot];
                    //  weights[xRoot] = 1
                    //  weights[yRoot = 1
                    //  weights[x] = m
                    //  weights[y] = n
                    //  value = m / n
                    //  合并以后
                    //  weights[xRoot] = 1
                    //  weights[x] = m
                    //  weights[y] = m / value
                    //  weights[yRoot] =  m / (value*n)
                    weights[yRoot] = weights[x]  / (weights[y] * value);
                } else {
                    parents[xRoot] = yRoot;
                    size[yRoot] += size[xRoot];
                    //  weights[xRoot] = 1
                    //  weights[yRoot = 1
                    //  weights[x] = m
                    //  weights[y] = n
                    //  value = x / y
                    //  合并以后
                    //  weights[yRoot] = 1
                    //  weights[y] = n
                    //  weights[x] = n * value
                    //  weights[xRoot] = (value*n) / m
                    weights[xRoot] = weights[y] * value / weights[x];
                }
            }
        }

查找权重方法

        public double isConnected(int x, int y) {
            int xRoot = find(x);
            int yRoot = find(y);
            if (xRoot == yRoot) {
                return weights[x] / weights[y];
            } else {
                return -1.0d;
            }
        }

要特别注意的一点是，因为压缩路径以后的并查集只有两层，根节点的权为1，所以执行find函数的时候，即便每次都要向上查询根节点，并且乘以根节点的权，得到的还是自己本该有的权。

Tips:并查集的操作时间复杂度

这里的α 表示阿克曼函数的反函数，在宇宙可观测的 n 内（例如宇宙中包含的粒子总数），α(n) 不会超过 5。