拓扑排序(Topological sort),又称 Topological order。实际上,它并不是一个纯粹的排序算法,它只是针对某一类图,找到一个可以执行的线性顺序。
给定一个包含 n 个节点的有向图 G,我们给出它的节点编号的一种排列,如果满足:
对于图 G 中的任意一条有向边 (u, v),u 在排列中都出现在 v 的前面。
那么称该排列是图 G 的「拓扑排序」。
- 假设图G中存在环,x1、x2、x3、xn和x。那么根据定义,x1要排列在xn前面,xn又要排列在x1前面,无法满足条件。
- 如果图G中不存在环,也就是说图G是有向无环图(Directed acyclic graph,DAG)。那么它的拓扑排序可能不止一种。
拓扑排序
首先我们需要图。图的两个要素是顶点和边。如下图所示:
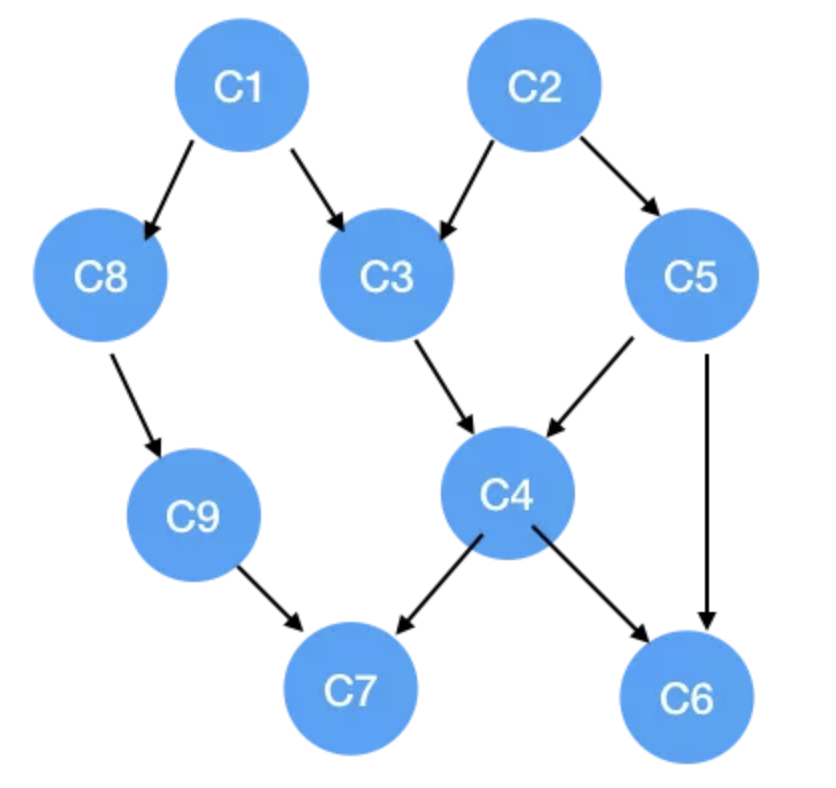
这种图叫做AOV(Activity On Vertex)网,在这种图里,顶点表示活动,边表示活动间的先后关系。
所以AOV网应该是一个DAG,否则某些活动会无法进行。那么所有活动可以排列成一个可行线性序列额,这个序列就是拓扑序列。
这个序列的实际意义是:按照这个顺序,在每个项目开始,都能保证它的前驱活动都已经完成,从而使工程顺序进行。
BFS解法详解
首先我们引入两个概念:
- 入度:顶点的入度是指“指向该顶点的边”的数量。
- 出度:顶点的出度是指“该顶点指向其他点的边”的数量。
所以,我们先执行入度为0的点,因为只有当它入度=0的时候,没有前驱活动,我们就可以执行它,不需要考虑别的活动。
所以具体做法是:
- 预处理得到每个点的入度
- 将入度为0的点放入队列中
- 从队列中依次取出前面的点(代表着以该点为顶点的指向其他点的边都消失了,也就是说该点的出度为0,所以,它指向的点的入度都要减1)
- 然后将入度变为0的点放入队列中,继续上一步
- 直到队列为空
Tips:这时候,如果还有节点的话,代表着节点的入度无法减少到0,也就是一定会有它指向的另外的点指向它自己,也就是有环的存在。
BFS示例代码:
class Solution {
// 存储有向图
List<List<Integer>> edges;
// 存储每个节点的入度
int[] indeg;
// 存储答案
int[] result;
// 答案下标
int index;
public int[] findOrder(int numCourses, int[][] prerequisites) {
edges = new ArrayList<List<Integer>>();
for (int i = 0; i < numCourses; ++i) {
edges.add(new ArrayList<Integer>());
}
indeg = new int[numCourses];
result = new int[numCourses];
index = 0;
for (int[] info : prerequisites) {
edges.get(info[1]).add(info[0]);
++indeg[info[0]];
}
Queue<Integer> queue = new LinkedList<Integer>();
// 将所有入度为 0 的节点放入队列中
for (int i = 0; i < numCourses; ++i) {
if (indeg[i] == 0) {
queue.offer(i);
}
}
while (!queue.isEmpty()) {
// 从队首取出一个节点
int u = queue.poll();
result[index++] = u;
for (int v: edges.get(u)) {
--indeg[v];
if (indeg[v] == 0) {
queue.offer(v);
}
}
}
if (index != numCourses) {
return new int[0];
}
return result;
}
}
DFS详解
思路是 对于一个节点 u,如果它的所有相邻节点都已经搜索完成,那么在搜索回溯到 u 的时候,u 本身也会变成一个已经搜索完成的节点。这里的「相邻节点」指的是从 u 出发通过一条有向边可以到达的所有节点。
我们用一个栈来存储已经搜索完成的节点,假设我们当前搜索到了节点 u,如果它的所有相邻节点都已经搜索完成,那么这些节点都已经在栈中了,此时我们就可以把 u 入栈。可以发现,如果我们从栈顶往栈底的顺序看,由于 u 处于栈顶的位置,那么 u 出现在所有 u 的相邻节点的前面。因此对于 u 这个节点而言,它是满足拓扑排序的要求的。
对于一个节点,它在搜索过程中有三种状态:
- 「未搜索」:我们还没有搜索到这个节点;
- 「搜索中」:我们搜索过这个节点,但还没有回溯到该节点,即该节点还没有入栈,还有相邻的节点没有搜索完成);
- 「已完成」:我们搜索过并且回溯过这个节点,即该节点已经入栈,并且所有该节点的相邻节点都出现在栈的更底部的位置,满足拓扑排序的要求。
具体操作是
-
我们将当前搜索的节点 u 标记为「搜索中」,遍历该节点的每一个相邻节点 v:
- 如果 v 为「未搜索」,那么我们开始搜索 v,待搜索完成回溯到 u;
- 如果 v 为「搜索中」,那么我们就找到了图中的一个环,因此是不存在拓扑排序的;
- 如果 v 为「已完成」,那么说明 v 已经在栈中了,而 u 还不在栈中,因此 u 无论何时入栈都不会影响到 (u,v) 之前的拓扑关系,以及不用进行任何操作。
-
当 u 的所有相邻节点都为「已完成」时,我们将 u 放入栈中,并将其标记为「已完成」。
DFS示例代码
class Solution {
// 存储有向图
List<List<Integer>> edges;
// 标记每个节点的状态:0=未搜索,1=搜索中,2=已完成
int[] visited;
// 用数组来模拟栈,下标 n-1 为栈底,0 为栈顶
int[] result;
// 判断有向图中是否有环
boolean valid = true;
// 栈下标
int index;
public int[] findOrder(int numCourses, int[][] prerequisites) {
edges = new ArrayList<List<Integer>>();
for (int i = 0; i < numCourses; ++i) {
edges.add(new ArrayList<Integer>());
}
visited = new int[numCourses];
result = new int[numCourses];
index = numCourses - 1;
for (int[] info : prerequisites) {
edges.get(info[1]).add(info[0]);
}
// 每次挑选一个「未搜索」的节点,开始进行深度优先搜索
for (int i = 0; i < numCourses && valid; ++i) {
if (visited[i] == 0) {
dfs(i);
}
}
if (!valid) {
return new int[0];
}
// 如果没有环,那么就有拓扑排序
return result;
}
public void dfs(int u) {
// 将节点标记为「搜索中」
visited[u] = 1;
// 搜索其相邻节点
// 只要发现有环,立刻停止搜索
for (int v: edges.get(u)) {
// 如果「未搜索」那么搜索相邻节点
if (visited[v] == 0) {
dfs(v);
if (!valid) {
return;
}
}
// 如果「搜索中」说明找到了环
else if (visited[v] == 1) {
valid = false;
return;
}
}
// 将节点标记为「已完成」
visited[u] = 2;
// 将节点入栈
result[index--] = u;
}
}
实际应用
最常考的就是选课系统,而拓扑排序最重要的应用就是关键路径问题,这个问题对应的是AOE(Activity on Edge)。
- AOE网络:顶点表示事件,边表示活动,边上的权重来表示活动所需要的时间。
- AOV网络:顶点表示活动,边表示活动之间的依赖关系。
在AOE网中,从起点到终点具有最大长度的路径称为关键路径,在关键路径上的活动称为关键活动。AOE网络一般用来分析一个大项目的工序,分析至少需要花多长时间完成以及每个活动能有多少机动时间。
其实对于一个任务之间有依赖关系的图,都是适用的。比如pom依赖引入jar包等。